农村的师傅的博客

一个迫于生计，无法放飞自我，导致喜欢上了前端开发，并即将成长为强者（指头发）的程序猿。

0%

算法-动态规划的一些总结

发表于 更新于 分类于

动态规划的一些学习和总结

什么是动态规划

动态规划通常叫他DP，写代码时，也用DP来表示，在我看来，动态规划重点其实是一个状态转移方程。他的本质上我是这么理解的：

对于一个问题，我们要找出其中的答案时，可以将该问题转换为一个和子问题相关问题来处理和解决。

那么什么是子问题？即一个问题可以拆解为若干个问题，而每个拆解出来的若干问题又可以继续拆解，一直拆解到我们可以直接解决或者知道答案的最小问题（即所说的动态规划的边界），此时再由最小子问题依次向上取递推来找到我们需要知道的最终问题。

动态规划常用来求解最优化问题，它们不仅包含重叠子问题，还具有另外两大特性：最优子结构、无后效性。

  • 最优子结构：问题的最优解包含其子问题的最优解。即，通过求解子问题的最优解，可以组合出原问题的最优解。
  • 无后效性：给定一个确定的状态，它的未来发展只与当前状态有关，而与过去经历的所有状态无关。

上面的解释和概念看看就好，我们接着看下面的例子可能比较好懂：

斐波那契数列，如果我们要知道第n个斐波那契数，我们该怎么算？

我们知道斐波那契数列的规律或者特性或者说是公式：第n个数 = 第n - 1个数 + 第n - 2个数，这就和我们上面所说的，找到第n个数就是我们需要解答的最终问题，而这个问题可以等价拆解为：我们需要找到第n-1和第n-2个斐波那契数，然后将其相加就得到了第n个斐波那契数，而如果我们把第n-1个斐波那契数作为一个问题时，他也可以被等价于：找到第n-1 - 1和n-1 - 2个斐波那契数之和，依次类推，直到我们知道第1个斐波那契和第2个斐波那契数是1和1。

从上面的解答中，你可以直接通过递归的形式计算出第n个斐波那契数：

1
2
3
4
5
6
7
8
9
function fib(n: number): number {
    if (n === 0) {
        return 0
    }
    if (n <= 2) {
        return 1
    }
    return fib(n - 1) + fib(n - 2);
}

上面是从找到第n个数开始去思考的写法，但是我们反过来去想，我们知道第1和第2个斐波那契数，那么由此，就可以得到第3个斐波那契数（根据上面的公式n3 = n2 + n1），而如果知道了第2和第3个斐波那契数，那就可以计算出第4个斐波那契数，那么依次类推，一直计算得到第n个斐波那契数：

1
2
3
4
5
6
7
8
9
10
function fib(n: number): number {
    /**
     * 斐波那契数列，第一个为0，第二个为1，第三个为1
     */
    const fibs = [0, 1, 1]
    for (let i = 3; i <= n; i++) {
        fibs[i] = fibs[i - 1] + fibs[i - 2]
    }
    return fibs[n]
}

上面代码中，我们将fibs数组视为斐波那契数列，数组的下标就表示第几个斐波那契数的值，第n个斐波那契数，即为fibs[n - 1] + fibs[n - 2]。

其实到了这里，我们就是将斐波那契数列的计算以动态规划的方式去实现了，回到我们上面说的动态规划的本质，将某个问题拆解为子问题，即找到问题和子问题的关系（此时你其实可以通过递归的方式去解决问题了）然后你再反过来从小的子问题的答案，去依次递推到最终你想要的那个问题的答案，这时候你就可以说完成了对该问题的动态规划。而上面的fibs[i] = fibs[i - 1] + fibs[i - 2]其实就是动态规划中常说的该问题的dp方程：dp[i] = dp[i - 1] + dp[i - 2]，或者说叫做状态转移方程。

其实到了这里，按照上面所说的，你已经找到问题和子问题了

其实对于一个问题的解答，其重点在于思考出解决方案中的方案，对于上面的斐波那契数列来说，你其实知道了这个问题的解决方案了，即可以对于第n个斐波那契数，它等于第n-1和n-2那个两个斐波那契数之和。所以，其实对于这个问题的dp方程，你也可以很容易去写出来，但是实际中，面对一个你第一次接触的问题，如果不是你之前了解过类似的，其实难点就在于如何找到这个问题的解法，也就是所谓的dp方程或者状态转移方程，每个问题或者每种类型的问题，其dp方程都是不一样的，这个我们下文举一些例子时也许你就能体会到了。

这里我们先来想另外一个事情：对于斐波那契数列这个问题来说，我用递归的方式去解决了，它算我们所说的动态规划吗？

其实不算，递归是递归，其实对于上面动态规划中所描述的“找到问题和子问题之间的关系”，它是一类问题的解法，而递归和动态规划是对于这类解法的一种实现。所以上面也提到，对于一个问题的解答，其重点在于思考出解决方案的方案，对于斐波那契数列问题来说，其解法为fib(n) = fib(n - 1) + fib(n - 2)，而我们在实现时可以利用递归的方式去实现，也可以使用动态规划的方式去实现。那么动态规划在实现时，有什么特别之处呢？我们同样以斐波那契数列的递归实现来举例：

1
2
3
4
5
6
7
8
9
function fib(n: number): number {
    if (n === 0) {
        return 0
    }
    if (n <= 2) {
        return 1
    }
    return fib(n - 1) + fib(n - 2);
}

在上面的递归实现中，我们假设n = 5，那么在实际递归运行中可以写出如下的调用方式：

  1. fn(5) = fn(4) + fn(3)
  2. fn(4) = fn(3) + fn(2)
  3. fn(3) = fn(2) + fn(1)

为了简便一点，我们只替换fn(4)就可以看出问题：fn(5) = ( fn(3) + fn(2) ) + fn(3)，此时对于fn(5)来说，fn(3)被重复调用了2次，而如果将fn(3)在替换一下：fn(5) = ( ( fn(2) + fn(1) ) + fn(2) ) + ( fn(2) + fn(1) )，你会发现，fn(2)重复调用了3次，fn(1)重复调用了2次，其实我们想一下，fn(3)和fn(2)本身被调用任意次数时，其结果都是一样的，而重复调用执行，就做了没必要的调用和计算。

那么我们是否可以想到将每次计算后的结果缓存起来，如果后续有相同的计算时，先去判断缓存中是否有该次调用的结果，如果有就直接返回缓存中的数据，这样是否就可以避免重复计算了，我们可以做如下改造：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
const cache = new Map<number, number>();
function fib(n: number): number {
    if (n === 0) {
        return 0
    }
    if (n <= 2) {
        return 1
    }
    if (cache.has(n)) {
        return cache.get(n)!
    }
    const result = fib(n - 1) + fib(n - 2);
    cache.set(n, result)
    return result
}

在上面的代码中，我们使用cache来缓存我们计算的每个斐波那契数的结果，这样在实际计算fn(5) = fn(4) + fn(3)时，由于fn(4)会计算出fn(3)，这样当fn(3)再次调用时，就可以直接返回其结果，而不用再去调用fn(2) + fn(1)了。这样我们就优化调用了重复调用和计算。

其实上面的优化方式也叫记忆化搜索，本质上就是对已经计算出的结果进行缓存，避免重复的计算。那么我们再想一下，上面的写法能否再改造一下呢？我们在写递归函数时，是从最开始的最终问题拆解为子问题，即fn(n) = fn(n - 1) + fn(n - 2)，那么我们从这个式子反过来去思考，通过第一个、第二个斐波那契数可以得到第三个，依次类推的话，就可以得到第n个斐波那契数，而这个所谓的反过来，就是递推，也是动态规划中的dp方程中非常重要的一个部分。

1
2
3
4
5
6
7
8
9
10
function fib(n: number): number {
    /**
     * 从已知的第0、1、2个斐波那契数依次递推到第n个
     */
    const fibs = [0, 1, 1]
    for (let i = 3; i <= n; i++) {
        fibs[i] = fibs[i - 1] + fibs[i - 2]
    }
    return fibs[n]
};

引用知乎中的递推和递归：
递推：从初值出发反复进行某一运算得到所需结果。—–从已知到未知，从小到达（比如每年长高9cm，20年180，30后270）
递归：从所需结果出发不断回溯前一运算直到回到初值再递推得到所需结果—-从未知到已知，从大到小，再从小到大(你想进bat，那么编程就的牛逼，就得卸载玩者农药，努力学习）。递归(Recursion)是从归纳法(Induction)衍生出来的。
作者：理工厨师
链接：https://www.zhihu.com/question/20651054/answer/668495939
来源：知乎

然而上面的式子还可以优化，我们发现，在上面的计算斐波那契数列的实现中，最重要的是这一句：fibs[i] = fibs[i - 1] + fibs[i - 2]，我们不难发现，每次循环时，所需要计算出的答案，仅仅和上一个斐波那契数和上上个斐波那契数相关，那么我们不需要一个数组来存储从0 - i的所有斐波那契数，只需要得到第i个即可（因为返回的结果中不需要返回他们），那么只需要两个变量来分别存放上一个和上上个斐波那契数，并且在每个循环中这两个变量进行更新即可。而两个变量作为一个常量空间，和n的大小无关，故上面的实现的空间复杂度O(1)。

它其实利用了滚动数组的技巧（滚动数组的核心思想是在处理问题时，不需要保存所有中间状态的完整数组，而是只保留与当前状态计算相关的若干个状态，通过不断更新和覆盖这些状态来模拟完整的计算过程，从而达到节省空间的目的。）

1
2
3
4
5
6
7
8
9
10
11
12
13
function fib(n: number): number {
    if (n <= 1) {
        return n
    }
    let last = 1
    let lastlast = 0
    for(let i = 2; i <= n; i++) {
        const value = last + lastlast
        lastlast = last
        last = value
    }
    return last
};

从上面的例子中，我们就完成了从一个问题的递归实现到动态规划实现的改造，总结一下就是，动态规划是基于递推的一种优化方案。如果你去找一下动态规划本身的常见定义：动态规划是一种通过把复杂问题分解为相对简单的子问题，并保存子问题的解来避免重复计算，从而解决优化问题的算法策略。它通常适用于具有最优子结构和子问题重叠性质的问题。这可能仍然无法理解，那么将其拆开两部分来看：

  1. 动态规划中的第一个部分把复杂问题分解为相对简单的子问题：这一句其实和上面中递归方法很像（这里指解决问题的方法，不是编程中的递归函数实现），将问题分解为子问题，并通过基于子问题的解可以得到最终问题的解。也就是说，动态规划所解决的问题，通常都可以转换为递归
    1. 这里递推和递归是思考问题解决方案的两个不同方向，一个是从最小问题一步步转换为最终问题，一个则是从最终问题一直拆分为最小问题。他们是两个相反的方向。
  2. 而第二部分保存子问题的解来避免重复计算，其实就是在具体代码实现中使用的优化方式（递归的记忆化搜索、递推的滚动数组）

也就是动态规划能够解决的问题，第一步你可以去思考如何将问题通过递归或者递推的方式将问题拆分为子问题，并找到他们之间的关系。然后再通过具体实现中的优化方式来优化其时间和空间复杂度。也就是第一步其实就是动态规划中最核心的内容，也是我认为动态规划最本质的东西。

对于一个问题：

  1. 思考：它能否以递推或者递归的思想来将问题拆分为一个个子问题，并通过找到子问题的解来得到最终问题的答案。
    1. 缩小问题规模，拆分为子问题
  2. 如果可以，理清问题和子问题之间的关系，并写出其中的关系式或者方程式（即动态规划中所说的dp方程，也叫状态转移方程）
    1. 其中拆分子问题通常会从由顶至底进行思考，然后再转换为由底至顶的方式
  3. 用记忆化搜索（递归）或者滚动数组（递推）等方式来优化具体实现中的时间或者空间复杂度

通过上面的例子，你应该对动态规划本身有了一个大概的了解。但是仅仅是这么说你可能仍然无法感受到动态规划中最重要的内容在实际中究竟是怎么来的，因为上面的斐波那契数列例子中动态规划最重要的状态转移方程（dp方程）可以说是明确告诉你了，而在实际的题目中，你可以需要自己去寻找这个状态转移方程，你可以假设一下，题目只给你一个数列（0,1,1,2,3,5,8），求第n个数是什么。这个时候你需要自己找到其数列的规律：哦，某个数的值等于上一个和上上个数的值之和。这其实才是你在用动态规划去解决实际问题时，最核心也是最难的点，这个所谓的规律你找不出，这个问题自然也无法用动态规划来写出来了。下面我就用我在写题目时的实际例子去说明吧。

例子：打家劫舍

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 1：

输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
     偷窃到的最高金额 = 1 + 3 = 4 。
示例 2：

输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
     偷窃到的最高金额 = 2 + 9 + 1 = 12 。

如果不看题解，我们从上面的问题去思考，如何通过动态规划去解决（假设你知道它能用动态规划解决了）

一开始不熟悉这类题时，可能会比较懵，一时也无法想到其中的状态转移方程或者该怎么去递推，那么先简单一点、暴力一点，先找到所有能抢的方案，并举例子、找规律（下面的方案中至少要抢1家店铺）：

  1. 如果有一家店铺，那么抢1 ，共1种方案
  2. 如果有两家店铺，那么抢1、2 ，共2种方案
  3. 如果有三家店铺，那么抢1、2、3或者13 ，共4种方案
  4. 如果有四家店铺，那么抢1、2、3、4或者13或者14或者24 ，共7种方案
  5. 如果有五家店铺，那么抢1、2、3、4、5或者13、14、15、24、25、35、135 ，共12种方案

我们知道从状态转移方程的重点就是找到问题和子问题之间的关系，且通过子问题的解来得到最终问题的解。那么如果只有5家店铺，能抢的方案数是12种，4家店铺能抢的是7种，3家店铺能抢的是4种，他们有什么联系吗？（1，2，4，7，12），貌似是：dp(5) = dp(4) + dp(3) + 1，为什么？

我们可以这么想：

  1. 有5家店铺时的所有方案，包含哪些情况？如何将其中的所有方案进行一个分类？
    1. 这里的分类也是一种场景的思考方式，因为这其实就是尝试将这个问题进行拆解，看能否将其和子问题关联起来
  2. 分类一：所有方案中，没有第5家店铺的那些方案，即排除了第5家店铺后的（1、2、3、4）4家店铺的所有方案
  3. 分类二：所有方案中，包含第5家店铺的方案有哪些？我们可以将其转换为：（1、2、3、4）家店铺的所有方案中没有第4家店铺的所有方案，因为他们都可以和5再组成新的方案。
  4. 分类三：只包含第5家店铺这一种方案

即：5家店铺的方案数 = 4家店铺的方案数 + 4家店铺的所有方案中没有第4家店铺的所有方案 + 1（仅包含5自身）

因为题目要求店铺不能相邻，所以包含了第5家店铺的方案必然不能出现第4家店铺。那么如何找到（1、2、3、4）4家店铺的所有方案中没有第4家店铺的所有方案？其实我们可以通过上面的思考过程再次转换一下：

  1. 有4家店铺时的所有方案，包含哪些情况？
  2. 分类一：所有方案中，没有第4家店铺的那些方案，即排除了第4家店铺后的（1、2、3）3家店铺的所有方案
  3. 分类二：所有方案中，包含第4家店铺的方案有哪些？我们可以将其转换为：（1、2、3）家店铺的所有方案中没有第3家店铺的所有方案，都可以和4再组成新的方案。
  4. 分类三：只包含第4家店铺这一种方案

好了，其实关键点已经出来了，就在分类一上，所有方案中，没有第4家店铺的那些方案，即排除了第4家店铺后的（1、2、3）3家店铺的所有方案

所以我们替换一下：5家店铺的方案数 = 4家店铺的方案数 + （1、2、3）3家店铺的所有方案 + 1（仅包含5自身）

从这里，我们就可以得到我们的状态转移方程了，对于有n家店铺时，其小偷可以偷取的所有店铺方案为：dp(n) = dp(n - 1) + dp(n - 2) + 1，dp(n)则表示n家店铺时，小偷可以偷取的所有店铺方案数。

这个时候，我们就做到了将针对n家店铺时，小偷的偷取方案数转换为了它的子问题：找到对n-1家店铺、n-2家店铺的偷取方案数。此时我们就搭建出了该问题动态规划的状态转移方程。但是题目是要找到偷窃的最高金额，我们现在只是找到了可以偷窃的方案数的动态规划状态方程，貌似还是没有解决实际问题。别急，这里只是讲解一个问题思考的方式。针对金额，我们同样可以思考：

  1. 所有方案中的金额最大值通常来说是需要比较每个方案的金额
  2. 现在我们将所有方案分为了3类，那么是否可以求出每一类方案下的最大金额，然后再对这三类方案的最大金额再次进行比较，是否就可以得到所有方案下的最大金额了？
  3. 第一类方案的最大金额其实就等于：n-1家店铺的所有方案中的最大金额
  4. 第二类方案的最大金额其实就等于：n-2家店铺的所有方案中的最大金额 + 第n家店铺本身的金额
  5. 而第三类方案仅仅是第n家店铺本身的金额，其肯定小于第二类方案的最大金额，故可以忽略

故，如果我们以小偷可以偷取的最大金额来作为状态，或者问题的求解，那么可以得到我们的状态方程：dp(n) = Max( dp(n - 1), dp(n - 2) + n )，dp(n)表示小偷偷取n家店铺时，可以偷取到的最大金额。

如此，针对该问题，我们就得到了在动态规划下最重要的状态转移方程。到了这，就可以开始最简单的编码了。

编码-递归-自顶向下

我们从动态规划得到的状态方程，通常都可以分为两种来实现，一种则是自顶向下，通常用递归+记忆化搜索的方式来实现和优化，一种是子底向上，一般用迭代+滚动数组来实现和优化。对于状态方程：dp(n) = Max( dp(n - 1), dp(n - 2) + n )，它本质上非常符合函数递归的写法，所以可以直接按照这个式子编写代码即可。而我们很容易就能知道dp(1)和dp(2)，所以，这里就是函数递归的中止边界。

递归+记忆化搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
function rob(nums: number[]): number {
    if (nums.length < 2) {
        return nums[0]
    }
    const cache = new Map<number, number>()
    function r(index: number): number {
        if (index === 0) {
            return nums[0]
        }
        if (index === 1) {
            return Math.max(nums[0], nums[1])
        }
        if (cache.has(index)) {
            return cache.get(index)!
        }

        const result =  Math.max(r(index - 1), r(index - 2) + nums[index])
        cache.set(index, result)
        return result

    }
    return r(nums.length - 1)
};

编码-递归-自底向上

在使用自底向上的方式实现时，我们就需要对我们的上面的dp方程进行一个转换，因为其形式符合递归，所以我们要将其转换为递推的形式，其实就是迭代的方式，已知dp(1)和dp(2)，那么就可以算出dp(3)、dp(4)…一直到dp(n)：

迭代：

1
2
3
4
5
6
7
8
9
10
function rob(nums: number[]): number {
    if (nums.length < 2) {
        return nums[0]
    }
    const dp: number[] = [nums[0], Math.max(nums[0], nums[1])]
    for (let i = 2; i < nums.length; i++) {
        dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
    }
    return dp[nums.length - 1];
};

迭代+滚动数组优化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
function rob(nums: number[]): number {
    if (nums.length < 2) {
        return nums[0]
    }
    let last1 = nums[0]
    let last2 = Math.max(nums[0], nums[1])
    let result = Math.max(last1, last2)
    for (let i = 2; i < nums.length; i++) {
        result = Math.max(last2, last1 + nums[i]);
        last1 = last2
        last2 = result
    }
    return result
};

例子：01背包问题

上面的重点是为了演示如何找到一个问题的状态转移方程，这是能写出动态规划代码的关键，而对于不同类型的问题，其动态规划方程也是不一样。这里再拿经典的01背包问题举例：一共有n件物品，第i（i从1开始）件物品的重量为w[i]，价值为v[i]。在总重量不超过背包承载上限W的情况下，能够装入背包的最大价值是多少？

我们先从暴力的角度去思考，每件物品最多只能选择一次，那么n件物品总共有多少种选择方案？且当每种方案的重量小于等于W时，才是符合要求的方案，且找出其所有方案中的最大值。这是最暴力的解法。

那么每种方案他们有什么共性或者特点？其实我们仍然可以按照上一个打家劫舍的问题思路来思考：假设共有n件物品（标记为0 - i）

  1. 对于从0 - i件物品进行选择时，所有满足条件的方案中，其方案都可以分为2类
  2. 第一类是包含了物品i的方案
  3. 第二类是不包含物品i的方案

此时我们直接思考每一类方案中，最大价值是如何确定的：

  1. 对于第一类：包含了物品i的方案，其最大价值 = v[i] + 排除了第i件物品后，剩余物品(0 - i-1)在剩余容量（W - w[i]）下能够能够装入的最大价值
  2. 对于第二类：不包含物品i的方案，其最大价值 = 排除了第i件物品后，剩余物品(0 - i-1)在容量W下能够能够装入的最大价值

这里的核心点在于识别出：在满足的方案中，包含了某一件物品，那么其他物品所能够放入的容量就等于可装入的总容量 - 该物品的容量

例如下面的数据：W总容量为80

w v i
10 50 0
20 120 1
30 150 2
40 210 3
50 240 4
  • 如果某一个方案中选择了容量为50价值为240的物品，那么在剩余物品（10、20、30、40）选择时，所能放下的总容量自然就变成了80-50=30了。
  • 如果某一个方案中不包含容量为50价值为240的物品，那么在剩余物品（10、20、30、40）选择时，所能放下的总容量仍然是80

由此，我们就可以通过上面的分析，得出该背包问题的状态转移方程，dp(i，W)表示在包含了0 - i这几件物品中，总重量不超过W上限的情况下，能够装入背包的最大价值数：dp(i, W) = Max(dp(i - 1, W - w[i]) + v[i], dp(i - 1, W))

这里的动态方程，需要注意其中的边界：

  1. 如果总容量W本身小于w[i]，那么该物品本身就无法放入到背包中，那么只剩下dp(i - 1, W)这一种情况
  2. 当i = 0时，即只有一个物品了，那么判断其容量W，是否大于等于该物品的容量w[i]，如果满足，则直接返回v[i]，否则返回0表示不能放入，其价值为0

上面是一种简单的dp方程，你可以直接基于该dp方程来通过递归函数来实现，并使用记忆化搜索的优化。而如果通过递推迭代的方式，上面的dp方程则需要改动一下：dp[i][j] = Max(dp[i - 1][W - w[i]) + v[i], dp[i - 1][W])，dp[i][j]表示对于可选的0-i件物品，总容量为j时，其最大价值。 这通常也就是所说的填充dp表（dp[i][j]，i从物品数n来进行迭代，j从目标的最大价值W来进行迭代（迭代嵌套），所以时间和空间复杂度都是O(n*W)。

迭代的写法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
function bag(w: number[], v: number[], k: number): number {
    const dp: number[][] = []

    for (let i = 0; i < w.length; i++) {
        dp[i] = [0]
        for (let j = 1; j <= k; j++) {
            const subWeight = j - w[i]
            if (subWeight >= 0) {
                // 可以放入背包
                dp[i][j] = Math.max(dp[i - 1]?.[j] || 0, (dp[i - 1]?.[subWeight] || 0) + v[i])
            }
            else {
                // 不能放入背包
                dp[i][j] = dp[i - 1]?.[j] || 0
            }
        }
    }

    return dp[w.length - 1][k]

};

在上面的01背包问题中，重点仍然是需要找出问题和子问题之间的关系，其规律在不同问题中都不尽相同，这才是动态规划去解决实际问题时最大的难点。有可能你找不出问题的拆解方式，或者其拆解方式不是最优的，下面这个例子就可以看到，我在做这个题目时，也找出了自认为其该问题的问题规律，也将其拆解为了子问题，但是它的拆解方式并非最优。

例子：最大正方形

leetcode

有了之前题目的经验，我当时是直接尝试去拆解子问题：

  1. 先找方案，n * m组成的矩阵，所有的正方形方案是什么
  2. 对于第(n,m)所组成的矩形来说，所有包含的所有正方形方案可以分为：
  3. 包含了第(n,m)元素的的正方形方案，和不包含第(n,m)元素的正方形方案
  4. 不包含第(n,m)元素的所有正方形方案，其实就是第(n-1,m)、（m，n-1）矩阵中所有正方形方案之和再减去（n-1，m-1）矩阵中所有正方形方案

由于主要是判断其最大正方形面积，所以方案重不重复不重要，故当时我写出状态关系为：

fn(n, m) = max([n, m], fn(n-1, m), fn(n, m-1))

由于我一开是从方案数的角度去考虑，并找出了m*n的矩形中，所有可以组成满足题意的正方形的方案数，故我仍然从这个角度去尝试找出最大正方形的状态方程：

dp方程：dp[i][j] = Max(maxSquare(i, j), dp[i - 1][j], dp[i][j - 1])

上面的dp方程中，maxSquare(i, j)是指，以i,j元素为右下角所组成的所有正方形的最大面积，对应于：包含了第(n,m)元素的的正方形方案中的最大正方形

示例

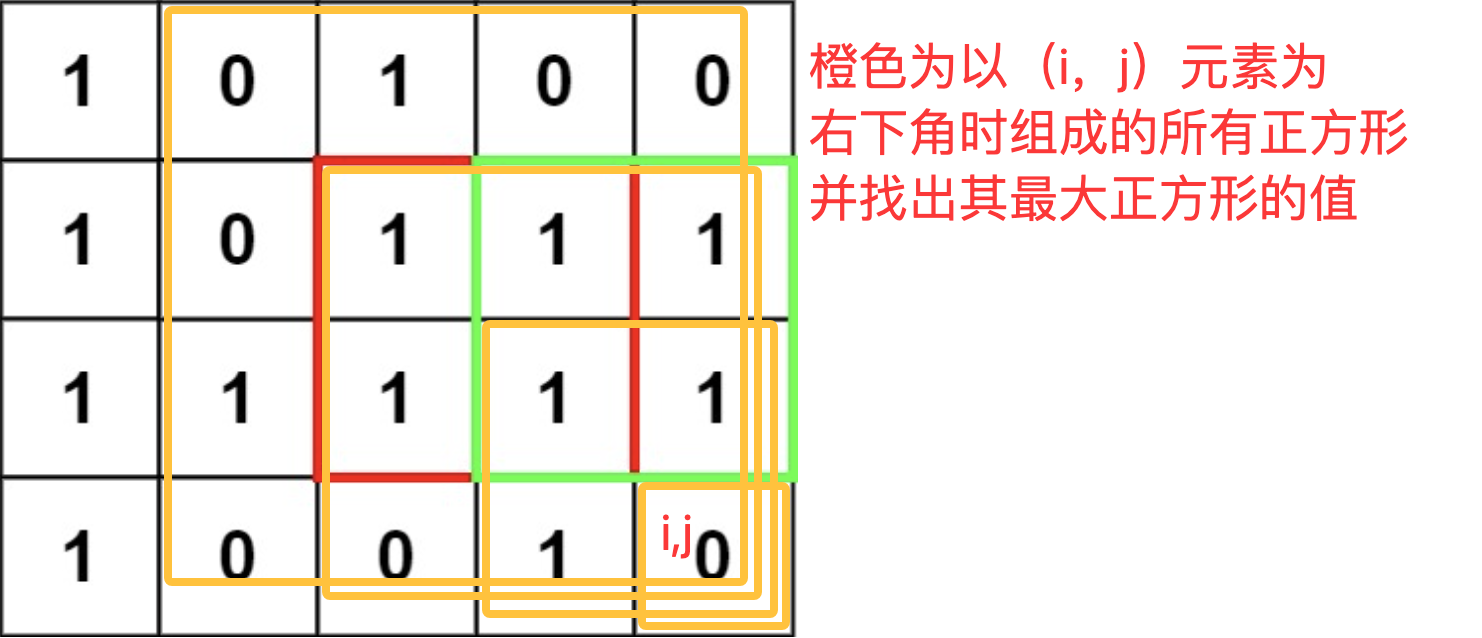
此时我写出的代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
function maximalSquare(matrix: string[][]): number {
    const dp: number[][] = []

    for (let i = 0; i < matrix.length; i++) {

        dp[i] = []

        for (let j = 0; j < matrix[0].length; j++) {

            let tempNIndex = i
            let tempMIndex = j
            let maxSquare: number = 0
            // 计算maxSquare的值
            while (tempNIndex >= 0 && tempMIndex >= 0) {
                let isOk = true
                for (let k = 0; k <= i - tempNIndex; k++) {
                    if (matrix[k + tempNIndex][tempMIndex] !== '1' || matrix[tempNIndex][tempMIndex + k] !== '1') {
                        isOk = false
                        break
                    }
                }
                if (isOk) {
                    maxSquare = (i - tempNIndex + 1) * (j - tempMIndex + 1)
                    tempNIndex--
                    tempMIndex--
                }
                else {
                    break
                }
            }

            dp[i][j] = Math.max(
                maxSquare,
                dp[i - 1]?.[j] || 0,
                dp[i]?.[j - 1] || 0,
            )

        }

    }

    return dp[matrix.length - 1][matrix[0].length - 1]
};

上面的代码中，在leetcode的测试用例中都能够通过，然而，最终提交时，却超时了。我一开始我还以为是当时写的代码逻辑没有优化导致的超时，但是最后我发现实在优无可优，且仍然在最后的2个用例中超时了。这时候我意识到，可能是我的思路错了，或者说我写出的dp方程出了问题，但是我一时也无法找到问题在哪，因为在逻辑上，其子问题的拆解是正确的，后来看到答案后，我才知道，在逻辑上，我的dp方程是对的，但是不是最优的，或者没有继续寻找规律来达到最优，每个问题都有不同的解法，算法题还有暴力和非暴力两种解法呢，问题拆解为子问题的方式和思考方向有不同可能太正常了，但是最终得出来的dp是否合理，这也是动态规划中很难直接说明的东西。

另外一种dp方程：dp(i,j)=min(dp(i−1,j),dp(i−1,j−1),dp(i,j−1))+1

leetcode中的证明过程

上面的dp方程中，省下了所谓的计算以（i，j）为右下角的所有正方形最大值的计算步骤，仅仅只是改动一下计算方式，节省了大量的计算，就和数学中的公式一样，更简洁的公式使用和计算起来会更简单，然而重点则在于，你能否找出最适合该问题的最优的那个公式。

结语

到这里，关于动态规划的学习，暂时就告一段落了，在你明白动态规划的本质之后，剩下的就是多做题来训练巩固和练习了。动态规划虽然解决的是一类问题，但是每类问题所涉及的状态转移方程都是不一样的。而其中的每个dp定义，其实也可以根据题目本身的需求来由我们自己定义其状态的含义，并以此找出dp方程。